What is DDSP?#
Aiming to address the challenges posed by neural audio synthesis, one line of research explored the integration of domain knowledge from speech and musical instrument acoustics, and digital signal processing, into neural networks. This was achieved by implementing the building blocks of signal processing algorithms using an automatic differentiation framework such as TensorFlow, PyTorch, or Jax. These implementations could then be combined with a neural network. In the forward pass, the network’s outputs are passed to the differentiable signal processors, which produce an output over which a loss is computed. In the backward pass, the gradients of the signal processors’ outputs with respect to the neural network’s outputs are computed.
For example, a neural network might output a value which is used as the cutoff frequency of a filter, which is implemented differentiably. During training, a loss function is computed on the output of the filter and, using the backpropogation algorithm, its gradient with respect to the neural network’s parameters is computed. In order to perform this computation, the derivative of the filter’s output with respect to its cutoff frequency must be evaluated. That is to say, the filter forms a part of the computation graph, and its gradient is a factor of the chain rule decomposition of the loss gradient.
The following figure gives a high level overview of the general structure of many DDSP synthesis systems.
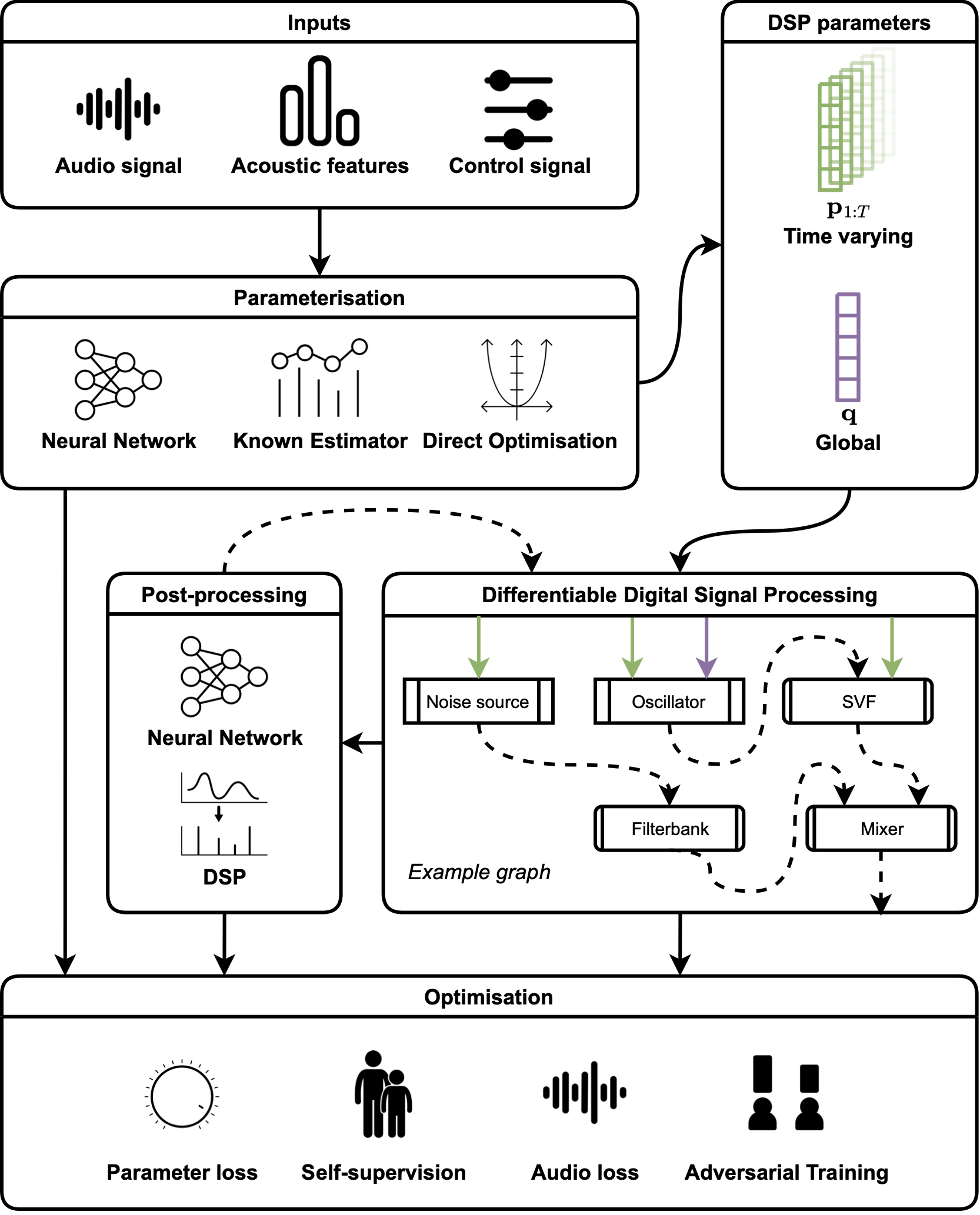
Fig. 3 A high level diagram illustrating the general structure of many DDSP synthesis systems. Taken from [HSF+23].#
Why is DDSP used?#
The applications of DDSP are varied, and we will go into further details on these in the next section. Nonetheless, there a number of recurring themes that appear in the literature as motivations for its use, as identified in our recent review paper [HSF+23]. DDSP appears to be most commonly applied when:
We have prior knowledge about the class of signal we are interested in. If we can express this prior knowledge in the form of a differentiable signal model, DDSP allows us to incorporate this knowledge into our network.
This can help in situations where neural networks struggle to reproduce a particular signal characteristic. For example, a differentiable harmonic oscillator bank allows phase alignment between successive windows [EHGR20], and a filtered white noise synthesiser enables a multi-band variational autoencoder to reconstruct aperiodic signal components [CE21]
This is also useful when we wish to perform self-supervised decomposition or analysis of an audio signal. This approach has been successfully used for source separation [SFRK+23] and pitch estimation [ESH+20].
We wish to infer the parameters of a particular signal processor or signal model. This is analogous to solving an inverse problem. In this case, our differentiable implementation allows us to perform parameter inference by gradient descent. This has been successfully applied for vocal tract area estimation [SudholtCXR23] and synthesiser sound matching [MS23].
We are concerned about inference-time latency. Producing every individual audio sample with a neural network is computationally costly. Whilst WaveNet’s sample-by-sample autoregression has been largely superseded by parallel methods, these are typically still too large to run in real-time in low-resource environments. Allowing a network to run at a slower frame rate while sample-by-sample audio synthesis is taken care of by efficient signal processors is a promising alternative.
We wish to allow human control over model outputs. In some cases, we may wish to allow a user to modify or otherwise interact with the outputs of a model. DDSP allows controls to be exposed in the form of interpretable intermediate parameters, as in MIDI-DDSP [WMD+22]
