Digital Synthesizer Modelling

In this chapter we’ll look at how a digital synthesizer for musical instrument synthesis can be implemented using the PyTorch library and how we can use gradient descent optimization to learn parameters for this synthesizer to match a target sound. We’ll build on what we learned in the introduction PyTorch chapter and work up to the development of a harmonic synthesizer similar to the one used by Engel et al. [EHGR20] to model instrument tones. Over the next few sections we’ll build up the core components of this harmonic synthesizer, starting from a simple sinusoidal oscillator. Our goal will be to use our synthesizer with gradient descent and an audio loss function to reproduce instrumental sounds from real recordings.

Can our synthesizer recreate these sounds?

Saxophone
Guitar
Violin
Vocal
Drum

Sinusoidal Modelling Synthesis

There are many different types of audio synthesis. One method that has been particularly fruitful in differentiable synthesis of musical instruments is sinusoidal modeling synthesis (SMS), initially developed by Serra and Smith [SS90] in the late 1980s. The core idea of SMS is based on Fourier’s theorem, which states that any sound can be decomposed into a set of sinusoidal basis components. SMS leverages this concept within an analysis-synthesis pipeline to model instrumental sounds by summing together sets of time-varying sinusoidal components.

Engel et al. [EHGR20] used a variant of a sinusoidal modelling synthesizer called a harmonic synthesizer, which essentially restricts the sinusoidal components to be integer multiples of a fundamental frequency, and made it differentiable. Engel et al. motivated this decision based on the knowledge that most musical sounds are periodic in nature and that embedding sinusoidal oscillators within a neural audio synthesizer provides a useful inductive bias towards the generation of those sounds.

In this chapter we will look at developing this differentiable harmonic synthesizer proposed by Engel et al.

If we look at the full model diagram from the original DDSP paper by Engel et al. [EHGR20], we are going to focus on developing the block component labelled Harmonic Audio and look at how we can use the Multi-Scale Spectrogram Loss to learn parameters to match the sounds we introduced above!

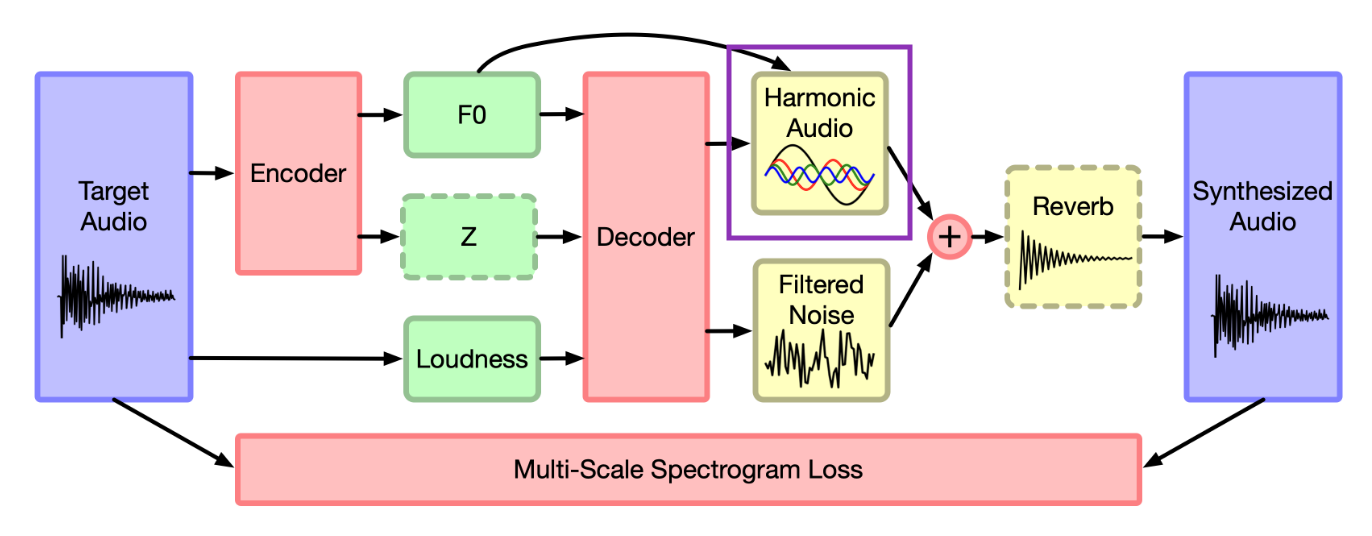
Fig. 6 DDSP model diagram, from the original DDSP paper by Engel et al.

Sinusoidal modelling is also just one of many synthesis methods that we can model differentiably. Some of these alternative methods will be overviewed and we will also introduce a couple open-source libraries which have implemented some core signal processing objects into composable differentiable modular synthesizers.

References

EHGR20(1,2,3)

Jesse Engel, Lamtharn (Hanoi) Hantrakul, Chenjie Gu, and Adam Roberts. DDSP: Differentiable Digital Signal Processing. In 8th International Conference on Learning Representations. April 2020.

SS90

Xavier Serra and Julius Smith. Spectral Modeling Synthesis: A Sound Analysis/Synthesis System Based on a Deterministic Plus Stochastic Decomposition. Computer Music Journal, 14(4):12–24, 1990. URL: www.jstor.org/stable/3680788 (visited on 2019-12-21), doi:10.2307/3680788.